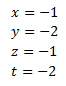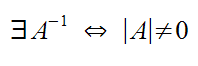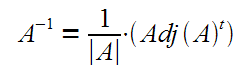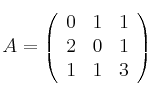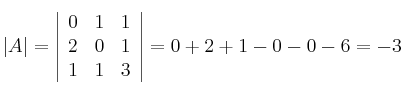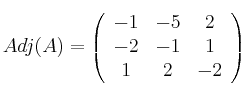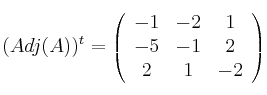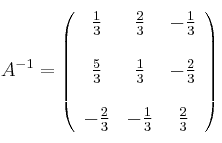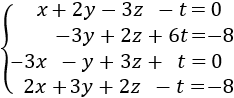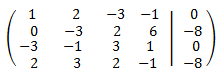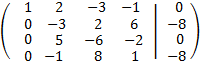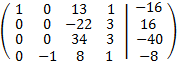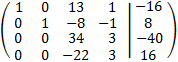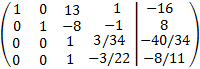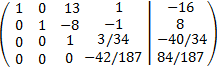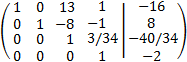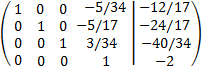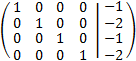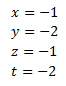Se llama matriz inversa de una matriz cuadrada A, y se expresa A-1, a la única matriz que cumple que:
A·A-1 = I = A-1·A
Es decir, la matriz inversa de A es la única matriz que al multiplicarla por ella obtenemos la matriz identidad del orden correspondiente.
La matriz inversa no siempre existe, para que exista, es condición necesaria y suficiente que el determinante de la matriz sea distinto de cero:
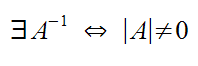
Aunque existe otro procedimiento para calcular la inversa a través de transformaciones elementales ( método de Gauss), la formula con la que se calcula la matriz inversa es:
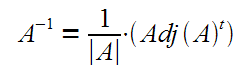
PROPIEDADES DE LA MATRIZ INVERSA
1. La matriz inversa si existe es única.
2. (A-1)-1 = A, es decir, la inversa de la inversa es la matriz inicial.
3. (A·B)-1 = B-1·A-1
4. |A-1| = 1 / |A|
Cálculo de la matriz inversa por definición
Supongamos que nos piden calcular la inversa de la matriz 
 1) Asignamos a los elementos de la matriz inversa (que desconocemos) letras: a, b, c, ..
1) Asignamos a los elementos de la matriz inversa (que desconocemos) letras: a, b, c, ..

 2) Planteamos la igualdad de la definición:
2) Planteamos la igualdad de la definición: 

 3) Resolvemos el producto de matrices
3) Resolvemos el producto de matrices 

 4) Igualamos elemento a elemento.
4) Igualamos elemento a elemento.



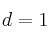
 5) Resolvemos los sistemas de ecuaciones resultantes
5) Resolvemos los sistemas de ecuaciones resultantes


Por tanto la inversa es 
MATRIZ INVERSA POR DETERMINANTE
Para aplicar determinante se debe aplicar la regla de Cramer que consiste en copiar las dos primeras filas hacia abajo o copiar las dos primeras columnas hacia la derecha, multiplicamos las diagonales superiores menos la diagonal inferior y así encontramos el valor del determinante principal.
Ejemplo
Vamos a calcular la inversa de la matriz 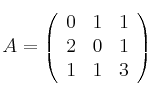
 Calculamos el determinante:
Calculamos el determinante: 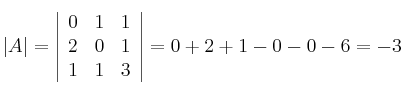
 Calculamos la matriz adjunta
Calculamos la matriz adjunta 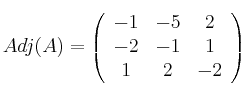
 Le hacemos la traspuesta:
Le hacemos la traspuesta: 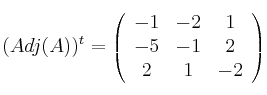
 Por último, dividimos por -3 (valor de |A|)
Por último, dividimos por -3 (valor de |A|)
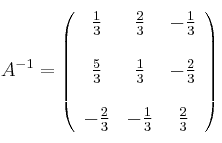
SISTEMAS RESUELTO POR ELIMINACIÓN
La matriz ampliada del sistema es
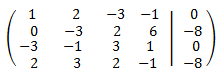
Realizamos operaciones elementales fila para obtener la matriz en forma escalonada reducida:
Sumamos a las filas tercera y cuarta la primera multiplicada por 3 y por -2, respectivamente:
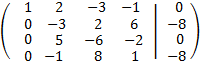
Sumamos a las filas primera, segunda y tercera la cuarta multiplicada por 2, -3 y 5, respectivamente:
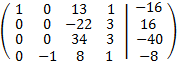
Multiplicamos la cuarta fila por -1 y la intercambiamos con la segunda:
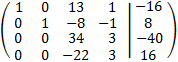
Multiplicamos las filas tercera y cuarta por 1/34 y -1/22, respectivamente:
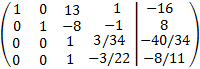
Le restamos la tercera fila a la cuarta:
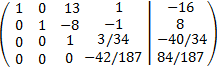
Multiplicamos la cuarta fila por -187/42:
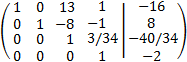
Le sumamos a las filas primera y segunda la tercera multiplicada por -13 y 8, respectivamente:
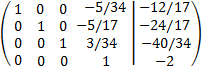
Le sumamos a las filas primera, segunda y tercera la cuarta multiplicada por 5/34, 5/17 y -3/34, respectivamente:
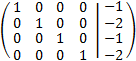
Su solución es