Se llama matriz inversa de una matriz cuadrada A, y se expresa A-1, a la única matriz que cumple que:
A·A-1 = I = A-1·A
Es decir, la matriz inversa de A es la única matriz que al multiplicarla por ella obtenemos la matriz identidad del orden correspondiente.
La matriz inversa no siempre existe, para que exista, es condición necesaria y suficiente que el determinante de la matriz sea distinto de cero:
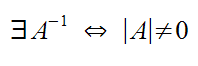
Aunque existe otro procedimiento para calcular la inversa a través de transformaciones elementales ( método de Gauss), la formula con la que se calcula la matriz inversa es:
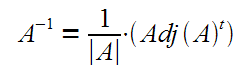
PROPIEDADES DE LA MATRIZ INVERSA
1. La matriz inversa si existe es única.
2. (A-1)-1 = A, es decir, la inversa de la inversa es la matriz inicial.
3. (A·B)-1 = B-1·A-1
4. |A-1| = 1 / |A|
Cálculo de la matriz inversa por definición

![]() 1) Asignamos a los elementos de la matriz inversa (que desconocemos) letras: a, b, c, ..
1) Asignamos a los elementos de la matriz inversa (que desconocemos) letras: a, b, c, ..
![]() 2) Planteamos la igualdad de la definición:
2) Planteamos la igualdad de la definición: ![]()

![]() 3) Resolvemos el producto de matrices
3) Resolvemos el producto de matrices ![]()

![]() 4) Igualamos elemento a elemento.
4) Igualamos elemento a elemento.![]()
![]()
![]()
![]()
![]() 5) Resolvemos los sistemas de ecuaciones resultantes
5) Resolvemos los sistemas de ecuaciones resultantes

Por tanto la inversa es 
Ejemplo
Vamos a calcular la inversa de la matriz 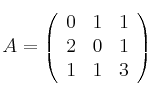
![]() Calculamos el determinante:
Calculamos el determinante: 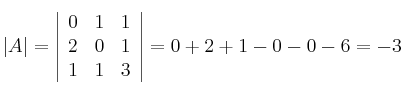
![]() Calculamos la matriz adjunta
Calculamos la matriz adjunta 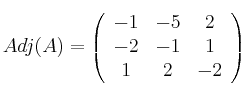
![]() Le hacemos la traspuesta:
Le hacemos la traspuesta: 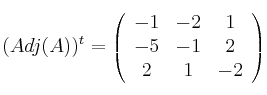
![]() Por último, dividimos por -3 (valor de |A|)
Por último, dividimos por -3 (valor de |A|)
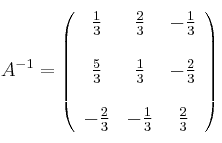
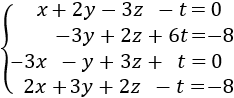
La matriz ampliada del sistema es
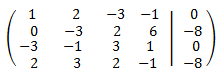
Realizamos operaciones elementales fila para obtener la matriz en forma escalonada reducida:
Sumamos a las filas tercera y cuarta la primera multiplicada por 3 y por -2, respectivamente:
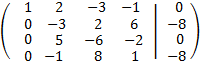
Sumamos a las filas primera, segunda y tercera la cuarta multiplicada por 2, -3 y 5, respectivamente:
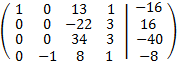
Multiplicamos la cuarta fila por -1 y la intercambiamos con la segunda:
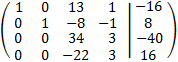
Multiplicamos las filas tercera y cuarta por 1/34 y -1/22, respectivamente:
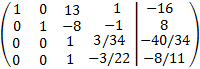
Le restamos la tercera fila a la cuarta:
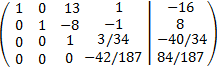
Multiplicamos la cuarta fila por -187/42:
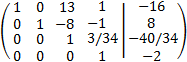
Le sumamos a las filas primera y segunda la tercera multiplicada por -13 y 8, respectivamente:
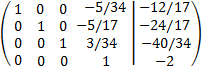
Le sumamos a las filas primera, segunda y tercera la cuarta multiplicada por 5/34, 5/17 y -3/34, respectivamente:
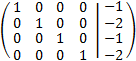
Su solución es
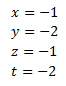







No hay comentarios.:
Publicar un comentario